pylist
127. Topological Sorting
Given an directed graph, a topological order of the graph nodes is defined as follow:
For each directed edge A -> B in graph, A must before B in the order list. The first node in the order can be any node in the graph with no nodes direct to it. Find any topological order for the given graph.
You can assume that there is at least one topological order in the graph.
Learn more about representation of graphs
Example
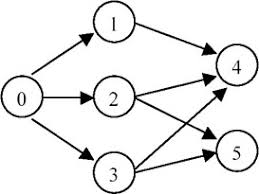
For graph as above, the topological order can be:
[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]
...
Solution
"""
Definition for a Directed graph node
class DirectedGraphNode:
def __init__(self, x):
self.label = x
self.neighbors = []
"""
class Solution:
"""
@param: graph: A list of Directed graph node
@return: Any topological order for the given graph.
"""
def topSort(self, graph):
# build in-degree dictionary
indegree = dict()
## init all indegrees
for node in graph:
indegree[node.label] = 0
## get indegrees
for node in graph:
for nei in node.neighbors:
indegree[nei.label] += 1
# topology sorting
## get node with 0 indegree
queue = deque() # node inside
for node in graph:
if indegree[node.label] == 0:
queue.append(node)
## BFS
tp_sort = []
while queue:
node = queue.popleft()
tp_sort.append(node)
for nei in node.neighbors:
indegree[nei.label] -= 1
if indegree[nei.label] == 0:
queue.append(nei)
## return tp_sort if tp sortable
if len(tp_sort) == len(indegree):
return tp_sort
else:
return []
Question to ask
- what if not DAG? I guess return []
- are labels unique? I guess unique
Special care:
- Check the length of tp_sot, if not the same as number of nodes, means not DAG, then return []