pylist
Leftmost Column with at Least a One
(This problem is an interactive problem.)
A binary matrix means that all elements are 0 or 1. For each individual row of the matrix, this row is sorted in non-decreasing order.
Given a row-sorted binary matrix binaryMatrix, return leftmost column index(0-indexed) with at least a 1 in it. If such index doesn’t exist, return -1.
You can’t access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface:
BinaryMatrix.get(row, col)returns the element of the matrix at index (row, col) (0-indexed).BinaryMatrix.dimensions()returns a list of 2 elements [rows, cols], which means the matrix is rows * cols.
Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.
For custom testing purposes you’re given the binary matrix mat as input in the following four examples. You will not have access the binary matrix directly.
Example 1:
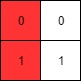
Input: mat = [[0,0],[1,1]]
Output: 0 Example 2:
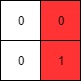
Input: mat = [[0,0],[0,1]]
Output: 1 Example 3:

Input: mat = [[0,0],[0,0]]
Output: -1 Example 4:
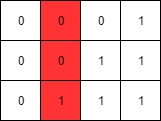
Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
Output: 1
Constraints:
rows == mat.length
cols == mat[i].length
1 <= rows, cols <= 100
mat[i][j] is either 0 or 1.
mat[i] is sorted in a non-decreasing way.
Solution
# """
# This is BinaryMatrix's API interface.
# You should not implement it, or speculate about its implementation
# """
#class BinaryMatrix(object):
# def get(self, x: int, y: int) -> int:
# def dimensions(self) -> list[]:
class Solution:
def leftMostColumnWithOne(self, binaryMatrix: 'BinaryMatrix') -> int:
size = binaryMatrix.dimensions()
up = size[1] - 1
all_zero = True
for i in range(size[0]):
temp = self.bisection(binaryMatrix, i, up)
if temp == -1:
continue
all_zero = False
up = temp
if all_zero:
return -1
return up
def bisection(self, mat, n_row, up):
low = 0
# return index of first 1
if up == 0:
return 0
if mat.get(n_row, low) == 1:
return 0
if mat.get(n_row, up) == 0:
return -1
while up - low > 1:
mid = low + (up - low) // 2
if mat.get(n_row, mid) == 1:
up = mid
else:
low = mid
return up