pylist
261. Graph Valid Tree
You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.
Return true if the edges of the given graph make up a valid tree, and false otherwise.
Example 1:
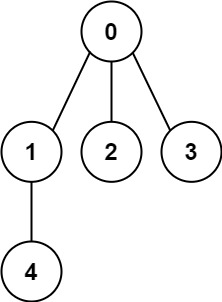
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true
Example 2:
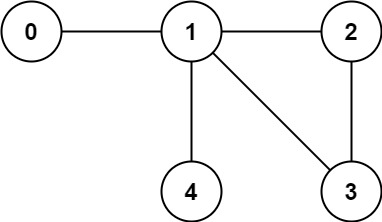
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false
Constraints:
- 1 <= n <= 2000
- 0 <= edges.length <= 5000
- edges[i].length == 2
- 0 <= ai, bi < n
- ai != bi
- There are no self-loops or repeated edges.
Solution
class Solution:
def validTree(self, n: int, edges: List[List[int]]) -> bool:
# test number of edges
if n != len(edges) + 1:
return False
# build graph
## build nodes
graph = [[] for i in range(n)]
## build edges
for e in edges:
graph[e[0]].append(e[1])
graph[e[1]].append(e[0])
# bfs to check if all connected
q = deque([0])
qed = set(q)
while q:
# pop
node = q.popleft()
# nothing to process about node
# add neighbors
for nei in graph[node]:
if nei not in qed:
q.append(nei)
qed.add(nei)
return n == len(qed) # if all nodes are enqueued
要点
- 图是树的条件
- 边数等于节点数-1
- 全连通(BFS来求)
- 因为是无向图,所以犯不着检查 有向无环图
- 因为是 0 到 n-1 所以图不需要 dict,用 list 就够了
- 建立图永远是先建立 node 再建立 edge
1,2
3
4,5
6
13
7
9
8
10
11
12
14
15
16
17
19
20
18
21
22
23
24
25